Left atrium segmentation and local maximas

I have been lately looking at the paper 'Automatic Left atrium segmentation by Cutting Blood pool at narrowings' by Matthias John et. al. My attempt to implement the method is still under-way. The 'apparent' simplicity of their method is the main reason behind the adoptation. Although not entirely non-trivial, their method is far less complicated than other attempts which have been made to segment the right atrium and ventricles.

The trick is to first determine the Euclidean distance transform (simply put for each voxel v, the distance to the closest unmarked voxel is the EDT for that voxel v. An unmarked voxel is that with a scalar value of 0). Here is a EDT color-coded map of the left atrium and surrouding heart structures and vessels. The red regions indicate high EDT, with gradually decreasing EDT as you move away from the center of the atrium (and other structures), which is indicated by other colors.


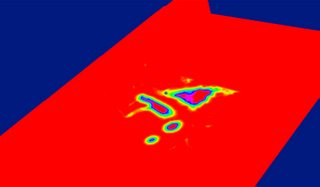
The image is however badly represented on red planes, which color-clashes with our red for high-EDT indicator.

After the EDT is determined, the next step is to locate the local maximas within the image. This is fairly trivial and not greatly processor intensive. For each voxel, a 14 or a 26-neighborhood is examined to determine if the voxel has the largest EDT in it's neighborhood. This would occasionally be the case, since there is almost always a neighbor with a larger EDT. Using a 26-neighborhood, my system yields around 220 local maximums. If you use a 10x10x10 neighborhood, you will only end up with 8 local maximums. The local maximums usually occur at the bary-center of the structures, indicating the deepest points in the structure.

Once the local-maximums have been determined, the subsequent step is to assign every voxel to a basic component. A basic component is a subset of the image. I like to think of it as the k-th partition of the image, where the image can be divided into n partitions with each partition being called a basic component. Each voxel ends up in one of the n partitions. The partitions are divided according to the local-maximums, with each parition having a local-maximum at its bary-center (or simply center). A voxel belongs to a partition, iff by following its gradient we end up at that partition's center (a local max). We follow the voxel's steepest gradients (i.e. with the largest EDT value).

I have been trying to implement this and visualize how a voxel can be assigned to a basic component partition. The following image below shows some local-maxs and a path marked by a caterpillar-like object. This path has actually been traced by several spherical points, thus giving it the caterpillar-like look.


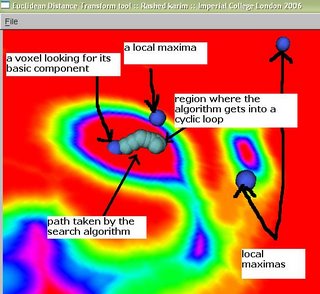
A voxel is looking for its basic component, and this is traced by the path (caterpillar-like) which is trying to reach the local-max right above it (marked in figure by 'a local max'). However, it gets into a never-ending cyclic loop. It is stuck between two voxels that have the largest values in both their neighborhoods. This can be easily avoided if we keep track of which voxels we have visited.