No to EM algorithm for computing Gaussian mixtures in background modeling

The mixture of Gaussians becomes necessary for modelling the background pixels, owing to the multi-modal distribution of pixel values that can occur in scenes recorded over time. Below are some examples taken from Stauffer. C. et al. paper, where he illustrates the red and green values of a certain pixel, taken from a scene viewed over time. Note the bi-modal distribution of the pixel's values. These images are taken from Stauffer et. al. "Adaptive background mixture models for real-time tracking"



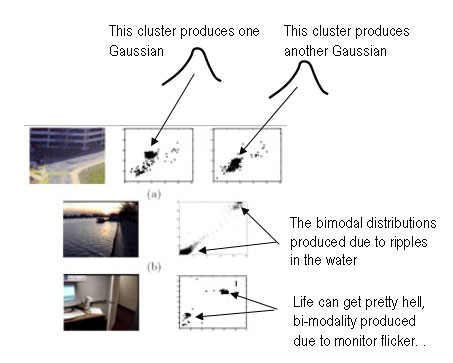
So now the question: given that we have these clusters of data sets, how do we come up with the Gaussian distributions? Normally, we would use the EM (Expectation maximization) algorithm to estimate the values of mu and sigma. A great tutorial/slides on EM can be found here.

EM achieves accuracy and "wraps" properly around the clusters after a number of iterations. In background modeling, each pixel is modeled as a mixture of gaussians. Hence, performing the EM on each pixel is a costly process, owing to the complexity of the EM algorithm. Stauffer et. al. suggests using an alternative approach as described in their paper "Adaptive background mixture models for real-time tracking". More on this, later.