Finally some segmentation. Flattening 3D volumes to 1D array

All this time I was thinking my region-growing procedure was running out of stack space. However, after some debugging I discovered that I was doing something wrong in the way I was transforming my 3D volume to a 1D array. Just sometime ago, when I was doing this course on Advanced graphics visualizations, I realized that you could store a 3D volume in a 1D array, and essentially the same goes with a 2D array. So if your 3D volume has dimensions x, y and z, a 1D array can be used to store the scalar value at any position (x,y,z). As you would have already imagined, the 1D array runs from index 0 to (x*y*z - 1). All you need is a mapping function that maps co-ordinates (x,y,z) to an index i in your 1D array. In your application, you might also require the inverse of this, i.e. from i to (x,y,z). The equations are quite straightforward:

Mapping function from (x,y,z) to array index i:

index i = (z * X * Y) + x + (X * y);

(where X, Y and Z are: 0<= x <=X and 0 <= y <= Y and 0 <= z <= Z)

and mapping from index i to (x,y,z):

z = i/(X * Y)

y = (i - z * X * Y)/(X)

x = i - (z * X * Y) - (y * X);

I was going wrong with these equations. Finally when I had them corrected, to ensure that these were correct, I wrote a verification program to test that the equations were invertible ( i.e. fg(x) = x if f = g^-1 ).

Both the recursive and non-recursive region-growing procedures now work fine. I had them tested on an artificial image of a brain MRI. I will be posting more results on the segmentation. Here are some preliminary results.

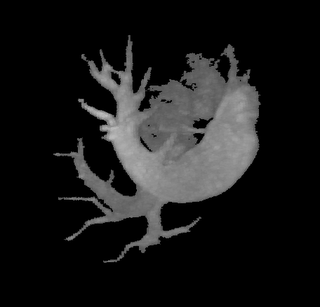
The procedure accepts both local and global thresholds. Local thresholds are thresholds imposed on the direct neighbors of a voxel, and these threholds vary from one voxel neighborhood to another. For e.g. I am using a threshold whereby every voxel in the region is allowed to include into the region a voxel in its neighborhood which is within a certain intensity +/- 5 for instance.

It so appears now, that if we try to pinpoint a small vessel and try to segment it using a small global threshold value, the entire volume gets segmented. However, the entire volume segmented comes out much "darker" than the original volume in the Maximum Intensity Projection (MIP) rendering.

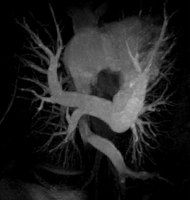
The image on the left is a MIP rendering of the segmented volume by using a seed point close to the atrium of the heart, and by using threshold values of 60 100. The image on the right is a MIP rendering of the segmented volume by using the same seed point, but using thresholds of 0 and 1000. The image on the right is essentially the entire volume and technically with nothing segmented.